Discover How Spinning Black Holes Bend Light and Reveal Repeated Images of Distant Galaxies
TL;DR
A new mathematical breakthrough explains why black holes create multiple images of distant galaxies by bending light. This bending, which allows light to loop around a black hole, results in distorted yet repeated images. The distance needed to see the next image of the same galaxy depends on the black hole’s spin. For spinning black holes, the images appear much closer together. These discoveries open doors to testing gravitational theories, and one day, we may witness delayed astronomical events, like a supernova explosion, occurring repeatedly due to light circling the black hole.
You’ve likely heard of black holes — those incredible regions of gravity so strong that even light can’t escape. You might also know that space and time act strangely near black holes; space gets bent out of shape.
Close to a black hole, space curves so dramatically that light rays bend, and if light gets near enough, it can be bent to the point of circling the black hole multiple times. As a result, when we observe a far-off galaxy (or any other celestial object), we might be fortunate enough to see several versions of the same image, though increasingly distorted.
Multiple versions of galaxies
This concept is illustrated below: a distant galaxy emits light in all directions. Some of its light passes near the black hole and is slightly bent, while other light comes even closer, looping around the black hole once before making its way to us, and so on. When looking near the black hole, we can see more versions of the same galaxy, each appearing closer to the hole’s edge.
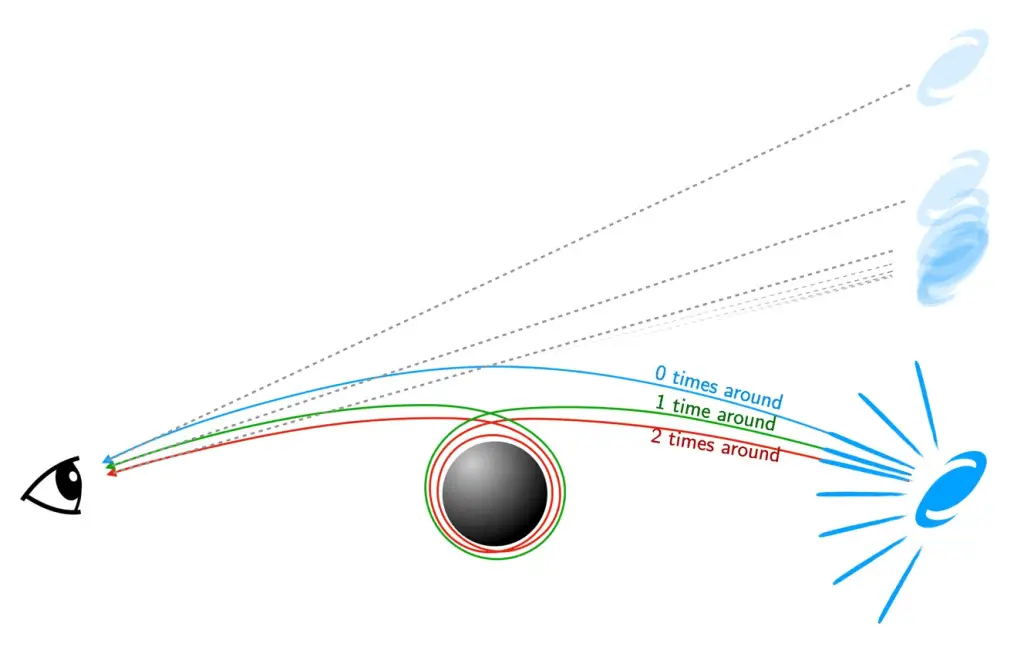
But how much closer to the black hole must you look to see the next image? The answer has been known for over 40 years: about 500 times closer (for math enthusiasts, it’s the “exponential function of two pi,” written as e^2π).
While calculating this factor is highly complex, until recently, we didn’t have a clear mathematical understanding of why it’s exactly that number. Now, thanks to some ingenious mathematical techniques, master’s student Albert Sneppen from the Cosmic Dawn Center — a basic research center linked to both the Niels Bohr Institute and DTU Space — has figured out the reason behind this.
“There’s something incredibly beautiful about now understanding why the images repeat so elegantly. Moreover, it opens up new possibilities for testing our knowledge of gravity and black holes,” says Albert Sneppen.
Proving something mathematically is not only rewarding on its own but also brings us closer to understanding this amazing phenomenon. The “500” factor directly stems from how black holes and gravity operate, meaning the repeated images can now serve as a tool to examine and verify gravity.
Rotating black holes
Sneppen’s method introduces an exciting new aspect: it can be applied not only to “simple” black holes but also to rotating black holes — and, in reality, all black holes spin.
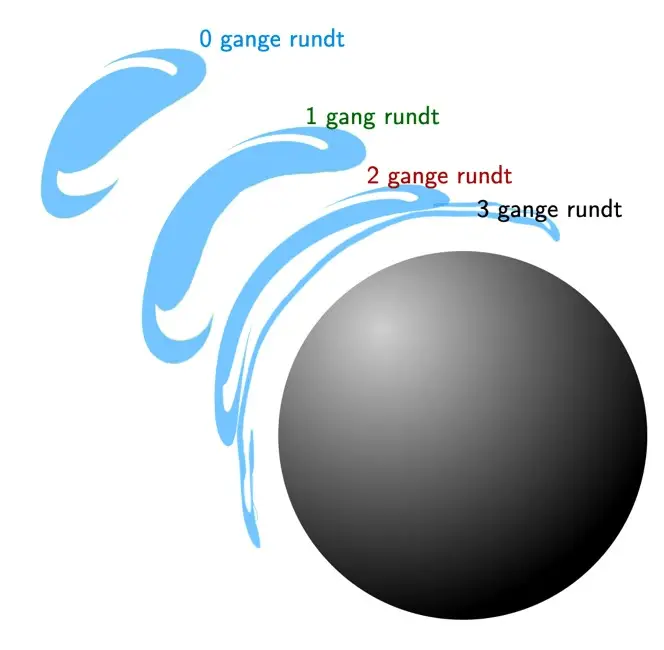
“It turns out that when the black hole spins really fast, you don’t have to look 500 times closer for the next image. It’s much less — the distance could be 50, or 5, or even just 2 times closer to the edge of the black hole,” explains Sneppen.
If each new image required looking 500 times closer to the black hole, the images would quickly be compressed into a single ring-like image, as shown in the figure on the right. This would make observing many images challenging. However, with rotating black holes, there’s more space for the “extra” images, meaning we may soon be able to confirm the theory through observations. This will allow us to learn more about both black holes and the galaxies behind them.
Additionally, the longer light takes to circle the black hole, the more “delayed” the images become. For instance, if a star in a background galaxy exploded as a supernova, we would be able to witness the explosion repeatedly.
Albert Sneppen’s article has just been accepted for publication in the journal Scientific Reports, and can be read here: Divergent reflections around the photon sphere of a black hole.




